The Ultimate Guide To Everything E-commerce
What is e?
In mathematics, e is the base of the natural logarithm. It is an irrational and transcendental number approximately equal to 2.71828. The letter e is also used to represent the mathematical constant approximately equal to 2.71828, which is the base of the natural logarithm.
E is also the fifth letter of the alphabet. It is a vowel and is pronounced differently depending on the word it is in. For example, in the word "bed," the e is pronounced with a short e sound, while in the word "feet," the e is pronounced with a long e sound.
- Get Inspired By Rachel Ray Top Recipes Shows And Lifestyle Tips
- Jennifer Lopezs Relationship With P Diddy A Comprehensive Guide
The constant e is used in many different areas of mathematics, including calculus, probability, and statistics. It is also used in physics, engineering, and other fields.
eIntroduction
Mathematical ConstantIntroduction
Natural LogarithmIntroduction
Uses in Mathematics and Other FieldsIntroduction
e
The letter e is the fifth letter of the alphabet and is a vowel. It is used in many different words, including the words "the," "be," and "me." The letter e can also be used to represent the mathematical constant approximately equal to 2.71828, which is the base of the natural logarithm.
- Mathematical constant: The letter e is used to represent the mathematical constant approximately equal to 2.71828, which is the base of the natural logarithm.
- Natural logarithm: The natural logarithm is a function that is used to find the power to which e must be raised to get a given number.
- Exponential function: The exponential function is a function that is used to find the value of e raised to a given power.
- Calculus: The letter e is used in calculus to represent the derivative of the exponential function.
- Probability: The letter e is used in probability to represent the probability of an event occurring.
- Statistics: The letter e is used in statistics to represent the expected value of a random variable.
- Physics: The letter e is used in physics to represent the charge of an electron.
- Engineering: The letter e is used in engineering to represent the efficiency of a machine.
These are just a few of the many different ways that the letter e is used in mathematics, science, and engineering. It is a versatile and important letter that plays a vital role in our understanding of the world around us.
- The Ultimate Guide To John Mccook Biography Career And Net Worth
- Meet The Robertson Family Jases Kids
Mathematical constant
The mathematical constant e is a fundamental number in mathematics and science. It is the base of the natural logarithm, and it arises in many different areas, including calculus, probability, and statistics. The letter e is also used to represent the mathematical constant approximately equal to 2.71828, which is the base of the natural logarithm.
The natural logarithm is a function that is used to find the power to which e must be raised to get a given number. It is also used to solve differential equations and to calculate the area under a curve.
The mathematical constant e is also used in probability and statistics. It is used to calculate the probability of an event occurring and to find the expected value of a random variable.
The mathematical constant e is a versatile and important number that plays a vital role in mathematics and science.
Natural logarithm
The natural logarithm is a function that plays a vital role in mathematics and science. It is used in many different areas, including calculus, probability, and statistics. The natural logarithm is also closely related to the mathematical constant e, which is approximately equal to 2.71828.
- Definition
The natural logarithm is the inverse of the exponential function. The exponential function is a function that raises e to a given power. The natural logarithm is the function that finds the power to which e must be raised to get a given number.
- Properties
The natural logarithm has a number of important properties. For example, the natural logarithm of 1 is 0, and the natural logarithm of e is 1. The natural logarithm is also a continuous and differentiable function.
- Applications
The natural logarithm is used in many different applications. For example, it is used to solve differential equations, to calculate the area under a curve, and to find the probability of an event occurring.
The natural logarithm is a versatile and important function that plays a vital role in mathematics and science. Its close relationship with the mathematical constant e makes it even more useful.
Exponential function
The exponential function is closely related to the mathematical constant e. In fact, the exponential function can be defined as the function that raises e to a given power. This means that the exponential function is the inverse of the natural logarithm.
The exponential function has a number of important properties. For example, the exponential function is always positive, and it is always increasing. The exponential function is also continuous and differentiable.
The exponential function is used in many different applications. For example, it is used to model population growth, to calculate compound interest, and to solve differential equations.
The exponential function is a powerful tool that can be used to model a wide variety of phenomena. Its close relationship with the mathematical constant e makes it even more useful.
Calculus
The exponential function is a fundamental function in mathematics. It is used to model a wide variety of phenomena, including population growth, compound interest, and radioactive decay. The derivative of the exponential function is also an important function. It is used to find the rate of change of a quantity that is changing exponentially.
The mathematical constant e is closely related to the exponential function. In fact, the exponential function can be defined as the function that raises e to a given power. This means that the derivative of the exponential function is also closely related to e.
The derivative of the exponential function is equal to e raised to the power of the exponent. This means that the derivative of the exponential function is always positive. This is because e is always positive.
The derivative of the exponential function is used in many different applications. For example, it is used to find the velocity of an object that is moving with exponential acceleration. It is also used to find the rate of growth of a population that is growing exponentially.
The connection between the exponential function, its derivative, and the mathematical constant e is a fundamental part of calculus. This connection is used to solve a wide variety of problems in mathematics and science.
Probability
The mathematical constant e plays a fundamental role in probability theory. It is used to define the probability density function of the normal distribution, which is one of the most important probability distributions in statistics. The normal distribution is used to model a wide variety of phenomena, including the distribution of heights in a population, the distribution of test scores, and the distribution of errors in measurements.
The probability density function of the normal distribution is given by the following equation:
f(x) = (1 / ((2))) e^(-(x - )^2 / (2^2))where: x is the random variable is the mean of the distribution is the standard deviation of the distributionThe letter e appears in the exponent of this equation. This indicates that the normal distribution is a type of exponential distribution. Exponential distributions are characterized by the fact that the probability of an event occurring decreases exponentially as the value of the random variable increases.The connection between e and probability is a fundamental part of statistics. This connection is used to solve a wide variety of problems in probability and statistics, including problems involving the normal distribution, the binomial distribution, and the Poisson distribution.
Statistics
In statistics, the expected value of a random variable is a measure of the central tendency of the variable. It is the average value that the variable is expected to take on over a large number of trials. The expected value is also known as the mean of the distribution.
The letter e is used to represent the expected value of a random variable because it is the base of the natural logarithm. The natural logarithm is a function that is used to find the power to which e must be raised to get a given number. The expected value is the power to which e must be raised to get the mean of the distribution.
The expected value is a useful measure of the central tendency of a random variable. It can be used to compare different distributions and to make predictions about the behavior of a random variable.
For example, the expected value of the number of heads that will be obtained when a coin is flipped 10 times is 5. This means that, on average, a coin will land on heads 5 times out of 10.
The expected value is a fundamental concept in statistics. It is used in a wide variety of applications, including the analysis of data, the design of experiments, and the development of statistical models.
Physics
The letter e is used in physics to represent the charge of an electron because it is the base of the natural logarithm. The natural logarithm is a function that is used to find the power to which e must be raised to get a given number. The charge of an electron is the power to which e must be raised to get the value of the charge of an electron.
The charge of an electron is a fundamental constant of nature. It is one of the most important constants in physics, and it plays a vital role in our understanding of the universe. The charge of an electron is used to calculate the force between two electrons, the force between an electron and a proton, and the force between an electron and a nucleus.
The connection between the letter e and the charge of an electron is a fundamental part of physics. This connection is used to solve a wide variety of problems in physics, including problems involving the force between charged particles, the energy levels of atoms, and the behavior of electrons in semiconductors.
Engineering
The letter e is used in engineering to represent the efficiency of a machine because it is the base of the natural logarithm. The natural logarithm is a function that is used to find the power to which e must be raised to get a given number. The efficiency of a machine is the power to which e must be raised to get the ratio of the output power to the input power.
- Efficiency
The efficiency of a machine is a measure of how well it converts input energy into output energy. The efficiency is always less than 100%, because some energy is always lost to friction and other inefficiencies.
- Power
The power of a machine is the rate at which it does work. The input power is the power that is supplied to the machine, and the output power is the power that is produced by the machine.
- Natural logarithm
The natural logarithm is a function that is used to find the power to which e must be raised to get a given number. The natural logarithm is also used to calculate the efficiency of a machine.
The connection between the letter e and the efficiency of a machine is a fundamental part of engineering. This connection is used to design more efficient machines and to improve the performance of existing machines.
FAQs on "e"
This section provides a compilation of frequently asked questions (FAQs) and their corresponding answers, offering clear and informative insights into the mathematical constant "e".
Question 1: What is the significance of the letter "e" in mathematics?
Answer: The letter "e" represents the base of the natural logarithm, an essential mathematical constant approximately equal to 2.71828. It holds fundamental importance in calculus, probability, and various other mathematical disciplines.
Question 2: How is "e" connected to the concept of natural logarithms?
Answer: The natural logarithm, denoted as "ln" or "log", is defined as the inverse function of the exponential function, which has "e" as its base. In simpler terms, the natural logarithm determines the power to which "e" must be raised to obtain a given number.
Summary: The mathematical constant "e" and the natural logarithm are closely intertwined concepts in mathematics. Their applications extend to a wide range of fields, including calculus, probability, statistics, and engineering.
Conclusion
The letter e is a fundamental mathematical constant that plays a vital role in a wide variety of fields, including mathematics, science, and engineering. It is the base of the natural logarithm, and it is used to define the exponential function. The letter e is also used to represent the charge of an electron and the efficiency of a machine.
The mathematical constant e is a fascinating and important number. It is a reminder of the power of mathematics and its ability to describe the world around us.
Article Recommendations
- Marlon Jacksons Enduring Legacy Exploring His Age And Impact On Music
- Waylon Jennings Country Music Legend
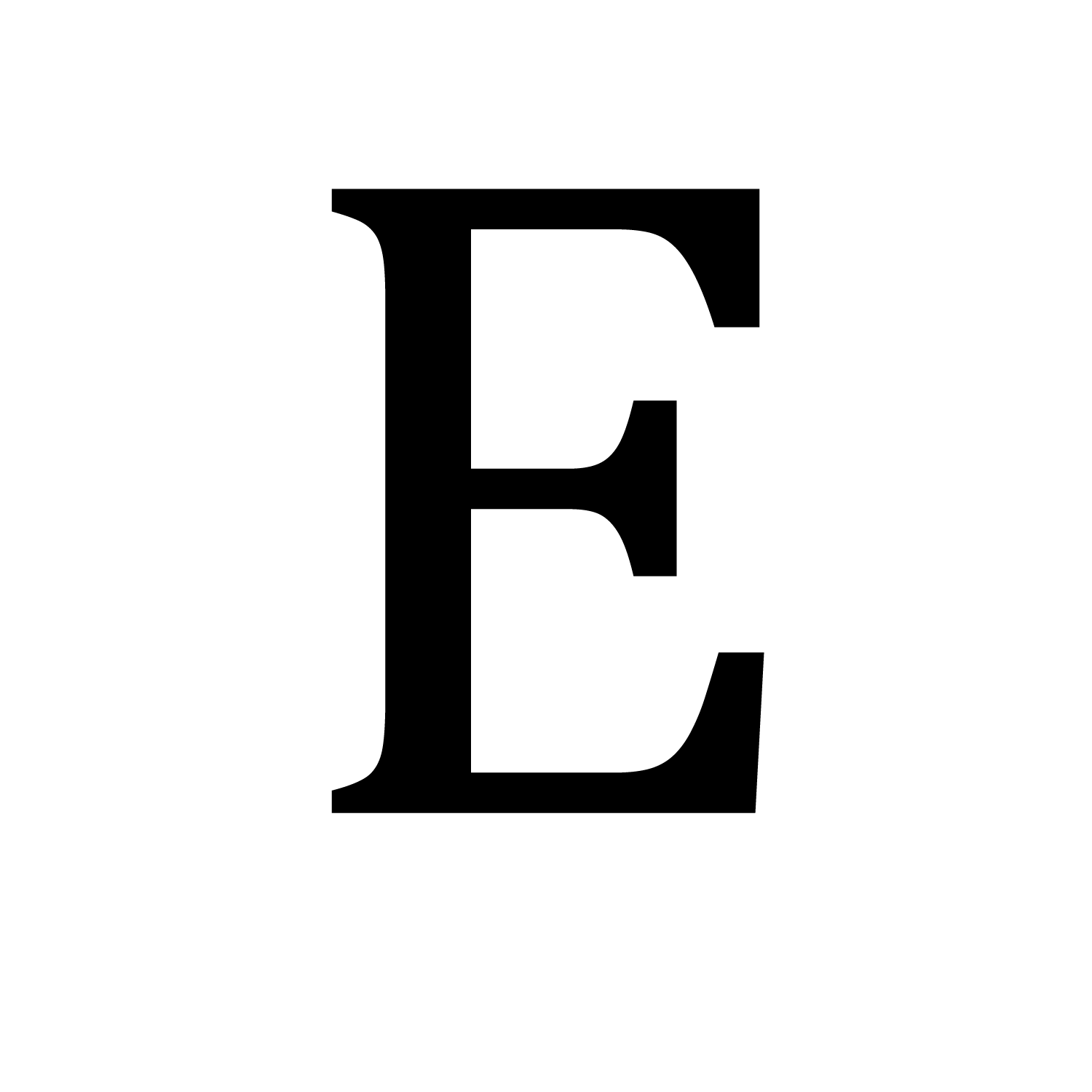


Detail Author:
- Name : Darlene Gleason I
- Username : ureinger
- Email : ofelia60@rosenbaum.org
- Birthdate : 1987-06-13
- Address : 7334 Skiles Meadows New Brisa, ME 39354
- Phone : +16403047643
- Company : McLaughlin, Grimes and Cruickshank
- Job : Respiratory Therapy Technician
- Bio : Aut voluptas inventore possimus quo. Consequatur repellendus eaque sit quaerat. Aut ut quam illum repellat et.
Socials
twitter:
- url : https://twitter.com/crystal_xx
- username : crystal_xx
- bio : Ipsam beatae earum animi reprehenderit omnis similique ea. Dolorem iste debitis facilis culpa dolorum eos. Ea explicabo natus fugit et.
- followers : 931
- following : 2148
tiktok:
- url : https://tiktok.com/@crystal5038
- username : crystal5038
- bio : Quo assumenda voluptatum quia dicta velit id fugiat.
- followers : 3786
- following : 2556
facebook:
- url : https://facebook.com/price2007
- username : price2007
- bio : Tempore consequatur numquam dolor facilis natus sit.
- followers : 3104
- following : 1324